A few days ago, Yannis Rizos posted 20 controversial programming opinions on the Programmers Community Blog. Judging by the comments on the blog, and on reddit and Hacker News, none of these opinions are considered all that controversial by the programming community at large. The problem stems from the fact that the opinions posted were selected from among the top-voted answers to Jon Skeet’s question What’s your most controversial programming opinion?, originally asked on Stack Overflow on January 2, 2009. People seem to have voted for answers they strongly agreed with, making those top answers some of the least controversial opinions you could gather.
I decided to take a different approach. What follows are some of the opinions that I found near the middle or at the end of the list. I tried to pick only answers where the author made an attempt at supporting their opinion, but as you can see some of these opinions were downvoted more heavily than they were upvoted by the Stack Overflow community. (I'll add that my own "controversial" opinion is that Jon's question is perhaps the best argument we have that these types of opinion polls simply do not work on Stack Overflow.)
1. Two lines of code is too many. (+20/-32) by Jay Bazuzi
If a method has a second line of code, it is a code smell. Refactor.
2. If it's not native, it's not really programming (+5/-15) by Mason Wheeler
By definition, a program is an entity that is run by the computer. It talks directly to the CPU and the OS. Code that does not talk directly to the CPU and the OS, but is instead run by some other program that does talk directly to the CPU and the OS, is not a program; it's a script. Read more
3. The "While" construct should be removed from all programming languages. (+6/-14) by seanyboy
You can easily replicate While using "Repeat" and a boolean flag, and I just don't believe that it's useful to have the two structures. In fact, I think that having both "Repeat...Until" and "While..EndWhile" in a language confuses new programmers. Read more
4. Copy/Pasting is not an antipattern, it fact it helps with not making more bugs (+4/-5) by serg
My rule of thumb - typing only something that cannot be copy/pasted. If creating similar method, class, or file - copy existing one and change what's needed. (I am not talking about duplicating a code that should have been put into a single method). Read more
5. Developing on .NET is not programming. Its just stitching together other people's code. (+7/-5) by Gerard
Having come from a coding background where you were required to know the hardware, and where this is still a vital requirements in my industry, I view high level languages as simply assembling someone else's work. Nothing essentially wrong with this, but is it 'programming'? Read more
6. The use of try/catch exception handling is worse than the use of simple return codes and associated common messaging structures to ferry useful error messages. (+11/-3) by Einstein
Littering code with try/catch blocks is not a solution.
Just passing exceptions up the stack hoping whats above you will do the right thing or generate an informative error is not a solution. Read more
7. Test Constantly (+15/-7) by PJ Davis
You have to write tests, and you have to write them FIRST. Writing tests changes the way you write your code. It makes you think about what you want it to actually do before you just jump in and write something that does everything except what you want it to do. Read more
8. Object Oriented Programming is absolutely the worst thing that's ever happened to the field of software engineering. (+34/-14) by Breton
The primary problem with OOP is the total lack of a rigorous definition that everyone can agree on. This easily leads to implementations that have logical holes in them, or language like Java that adhere to this bizarre religious dogma about what OOP means, while forcing the programmer into doing all these contortions and "design patterns" just to work around the limitations of a particular OOP system. Read more
9. C (or C++) should be the first programming language (+24/-5) by hansen j
The first language should NOT be the easy one, it should be one that sets up the student's mind and prepare it for serious computer science.
C is perfect for that, it forces students to think about memory and all the low level stuff, and at the same time they can learn how to structure their code (it has functions!)
C++ has the added advantage that it really sucks :) thus the students will understand why people had to come up with Java and C#.
10. Classes should fit on the screen. (+22/-7) by Jay Bazuzi
If you have to use the scroll bar to see all of your class, your class is too big.
Code folding and miniature fonts are cheating.
11. Making invisible characters syntactically significant in python was a bad idea (+43/-5) by Paul Wicks
It's distracting, causes lots of subtle bugs for novices and, in my opinion, wasn't really needed. About the only code I've ever seen that didn't voluntarily follow some sort of decent formatting guide was from first-year CS students. And even if code doesn't follow "nice" standards, there are plenty of tools out there to coerce it into a more pleasing shape.
12. Singletons are not evil (+42/-7) by Steve
There is a place for singletons in the real world, and methods to get around them (i.e. monostate pattern) are simply singletons in disguise. For instance, a Logger is a perfect candidate for a singleton. Additionally, so is a message pump. My current app uses distributed computing, and different objects need to be able to send appropriate messages. There should only be one message pump, and everyone should be able to access it. The alternative is passing an object to my message pump everywhere it might be needed and hoping that a new developer doesn't new one up without thinking and wonder why his messages are going nowhere. The uniqueness of the singleton is the most important part, not its availability. The singleton has its place in the world.
Saturday, September 1, 2012
Sunday, July 1, 2012
SICP 2.61 - 2.62: Sets as ordered lists
From SICP section 2.3.3 Example: Representing Sets
In exercises 2.59 and 2.60 we looked at how to represent sets as unordered lists. In the next two we'll look at representing sets as ordered lists, and at what benefits we get from the new implementation.
First, if elements in a set are guaranteed to be in order, we can improve the performance of
The original implementation of
Exercise 2.62 asks us to give a $O(n)$ implementation of
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
In exercises 2.59 and 2.60 we looked at how to represent sets as unordered lists. In the next two we'll look at representing sets as ordered lists, and at what benefits we get from the new implementation.
First, if elements in a set are guaranteed to be in order, we can improve the performance of
element-of-set by returning false as soon as we encounter an element of the set that's less than the value that we're looking for. All of the remaining elements are guaranteed to be smaller as well. This saves us on average half the number of comparisons from the previous implementation.
(define (element-of-set? x set)
(cond ((null? set) false)
((= x (car set)) true)
((< x (car set)) false)
(else (element-of-set? x (cdr set)))))
We get a more impressive improvement from intersection-set. In the old implementation using unordered lists we had to compare every element of each set to every element in the other set. This had a complexity of $O(n^2)$. With the elements of both sets in order we can reduce that all the way down to $O(n)$. This is possible due to the fact that if the car of one ordered set is smaller than the car of another ordered set, it has to be smaller than all the other elements and we can discard it right away.
(define (intersection-set set1 set2)
(if (or (null? set1) (null? set2))
'()
(let ((x1 (car set1)) (x2 (car set2)))
(cond ((= x1 x2)
(cons x1
(intersection-set (cdr set1)
(cdr set2))))
((< x1 x2)
(intersection-set (cdr set1) set2))
((< x2 x1)
(intersection-set set1 (cdr set2)))))))
Exercise 2.61 asks us to give an implementation of adjoin-set using the ordered representation. Like element-of-set?, our implementation of adjoin-set should require only half as many steps on average as the unordered representation.The original implementation of
adjoin-set made use of element-of-set? to check and see if the new element was already a member of the set. We no longer need to do this since we need to find the exact position in the set to insert the new element. As we scan through the set looking for the right position, we can simply return the set if we encounter the element we're trying to place.
(define (adjoin-set x set)
(cond ((null? set) (cons x '()))
((= x (car set)) set)
((< x (car set)) (cons x set))
((> x (car set)) (cons (car set)
(adjoin-set x (cdr set))))))
There are several different conditions, and we need to cover them all. First, since we're no longer using element-of-set, we need to check to see if the set itself is null or empty. Second, if the we encounter the element we're trying to add, we can just return the set. Next, if the element we're adding is smaller than the first element of the set, we can simply cons the new element to the beginning of the set. Last, if the new element is greater than the first element of the set, we join the first element followed by the adjoin-set of the new element and the rest of the set.
> (adjoin-set 3 null) (3) > (adjoin-set 3 '()) (3) > (adjoin-set 3 '(3 4 5)) (3 4 5) > (adjoin-set 3 '(4 5 6)) (3 4 5 6) > (adjoin-set 3 '(1 2 4 5)) (1 2 3 4 5) > (adjoin-set 3 '(0 1 2)) (0 1 2 3)Like
element-of-set?, this implementation should only scan through half the set on average before finding the correct insertion point for the new element.Exercise 2.62 asks us to give a $O(n)$ implementation of
union-set for sets represented as ordered lists. Since the two sets are in order, we can simply step through each set comparing the first elements of each. At each step we decide which of the first two elements to place in the resulting set.
(define (union-set set1 set2)
(cond ((null? set1) set2)
((null? set2) set1)
((= (car set1) (car set2))
(cons (car set1) (union-set (cdr set1) (cdr set2))))
((< (car set1) (car set2))
(cons (car set1) (union-set (cdr set1) set2)))
(else (cons (car set2) (union-set set1 (cdr set2))))))
Anyone familiar with the mergesort algorithm will quickly recognize that this implementation of union-set is almost exactly the same procedure as the merge subroutine. It's purpose is to quickly merge two sorted lists into one. The only difference is that the union-set implementation above only keeps one copy of duplicate elements.
> (define odds '(1 3 5 7)) > (define evens '(2 4 6 8)) > (define primes '(2 3 5 7)) > (union-set odds evens) (1 2 3 4 5 6 7 8) > (union-set odds primes) (1 2 3 5 7) > (union-set evens primes) (2 3 4 5 6 7 8)
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
Labels:
programming,
scheme,
sicp
Monday, May 28, 2012
SICP 2.59 - 2.60: Sets as unordered lists
From SICP section 2.3.3 Example: Representing Sets
Section 2.3.3 shows us several ways to represent sets in Scheme, starting with unordered sets. To start, we define what a 'set' is by specifying the operations that are to be used on sets. These are:
We represent a set as an unordered list by making sure no element appears more than once. The text provides the following implementations for representing sets as unordered lists.
We can define a few lists to test and see how these procedures work together.
Exercise 2.59 asks us to implement the
This implementation starts by checking to see if either set is null. If so, the other set is returned immediately. The procedure then checks to see if the first element of
Exercise 2.60 asks us what would need to change in the implementations above if we redefine 'set' to allow duplicate elements. For example, the set {1, 2, 3} could be represented as the list (2 3 2 1 3 2 2). We need to compare the efficiency of each of the new procedures with their original (non-duplicate) implementations. The exercise also asks if there are applications where the new representation would be preferred over the original.
The implementation of
Like
We have an interesting choice when it comes to
The result is different depending on which set has duplicate elements. This is because the original implementation checks each element of the first set independently to see if they're present in the second set. When the first set contains duplicates, so will the result. Since the instructions in the exercise are ambiguous (and being the typical lazy programmer that I am), I'm going to say that this implementation does not need to change.
Since
The penalty that we pay for these performance improvements is that sets now require more memory to accommodate duplicate elements. This representation would be preferred over the original in cases where we don't care about that added memory overhead, and where most of our operations are either
Related:
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
Section 2.3.3 shows us several ways to represent sets in Scheme, starting with unordered sets. To start, we define what a 'set' is by specifying the operations that are to be used on sets. These are:
element-of-set?- a predicate function that determines whether a given element is a member of a set.adjoin-set- takes an object and a set as arguments and returns the set that contains the elements of the original set and the adjoined object.intersection-set- computes the intersection of two sets, which is the set containing only elements that appear in both arguments.union-set- computes the union of two sets, which is the set containing each element that appears in either argument.
We represent a set as an unordered list by making sure no element appears more than once. The text provides the following implementations for representing sets as unordered lists.
(define (element-of-set? x set)
(cond ((null? set) false)
((equal? x (car set)) true)
(else (element-of-set? x (cdr set)))))
(define (adjoin-set x set)
(if (element-of-set? x set)
set
(cons x set)))
(define (intersection-set set1 set2)
(cond ((or (null? set1) (null? set2)) '())
((element-of-set? (car set1) set2)
(cons (car set1)
(intersection-set (cdr set1) set2)))
(else (intersection-set (cdr set1) set2))))
We can define a few lists to test and see how these procedures work together.
> (define odds '(1 3 5 7)) > (define evens '(2 4 6 8)) > (define primes '(2 3 5 7)) > (element-of-set? 5 odds) #t > (element-of-set? 5 evens) #f > odds (1 3 5 7) > (adjoin-set 9 odds) (9 1 3 5 7) > (intersection-set odds evens) () > (intersection-set odds primes) (3 5 7) > (intersection-set evens primes) (2)
Exercise 2.59 asks us to implement the
union-set operation for the unordered-list representation of sets.(define (union-set set1 set2)
(cond ((null? set1) set2)
((null? set2) set1)
((element-of-set? (car set1) set2) (union-set (cdr set1) set2))
(else (cons (car set1) (union-set (cdr set1) set2)))))
This implementation starts by checking to see if either set is null. If so, the other set is returned immediately. The procedure then checks to see if the first element of
set1 is an element of set2. If so, that element is discarded from the first set, and the union of the remaining elements of set1 and set2 are returned. If the first element of set1 is not an element of set2, it is included in the list returned by the procedure.> (union-set odds evens) (1 3 5 7 2 4 6 8) > (union-set odds primes) (1 2 3 5 7) > (union-set evens primes) (4 6 8 2 3 5 7)
Exercise 2.60 asks us what would need to change in the implementations above if we redefine 'set' to allow duplicate elements. For example, the set {1, 2, 3} could be represented as the list (2 3 2 1 3 2 2). We need to compare the efficiency of each of the new procedures with their original (non-duplicate) implementations. The exercise also asks if there are applications where the new representation would be preferred over the original.
The implementation of
element-of-set? doesn't need to change. It returns #t when it finds an element that matches the input element, otherwise it returns #f.
The implementation of adjoin-set is simplified by the new definition. Since we no longer need to check to see if the input element already exists in the set, we can just cons the element to the existing set.(define (adjoin-set x set) (cons x set))
Like
adjoin-set, union-set is also simplified by allowing duplicate elements.(define (union-set set1 set2) (append set1 set2))
We have an interesting choice when it comes to
intersection-set. The intersection of two sets under the original (non-duplicate) definition doesn't seem like it requires any change in implementation since duplicates are now allowed, not necessarily required. However, look what happens when you execute intersection-set with duplicate elements in the first set vs. the second set.> (define primes '(2 3 5 7)) > (define twos '(2 2 2)) > (intersection-set primes twos) (2) > (intersection-set twos primes) (2 2 2)
The result is different depending on which set has duplicate elements. This is because the original implementation checks each element of the first set independently to see if they're present in the second set. When the first set contains duplicates, so will the result. Since the instructions in the exercise are ambiguous (and being the typical lazy programmer that I am), I'm going to say that this implementation does not need to change.
Since
element-of-set? and intersection-set haven't changed, neither will their performance. Since adjoin-set and union-set no longer need to check for duplicate elements, the performance of both of these procedures is improved. The number of steps required by adjoin-set has gone from $O(n)$ to $O(1)$. The number of steps required by union-set has gone from $O(n^2)$ to $O(n)$.The penalty that we pay for these performance improvements is that sets now require more memory to accommodate duplicate elements. This representation would be preferred over the original in cases where we don't care about that added memory overhead, and where most of our operations are either
adjoin-set or union-set.Related:
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
Labels:
programming,
scheme,
sicp
Sunday, May 6, 2012
Which Open Source License?
I was doing a little research on open source software licenses with a student when I came across this flow chart.
I like the balance it strikes between being funny and still being at least somewhat useful and informative. Credit for the original flowchart goes to the creators Dan Bentley and Brian Fitzpatrick. (Thanks to @jldeev for pointing me to the chart.)
For a short break down of the key differences between some of the more popular software licenses, see Jeff Atwood's post Pick a License, Any License on the Coding Horror blog. The main point to take away from the article is that if you don't explicitly declare a license on software you publish, your code is copyrighted by default. To use the code people have to contact you and ask permission. So if you post a lot of code examples on your blog, take a few minutes to pick a license then add a notice to the footer of your site.
Labels:
licenses,
open source,
software
Sunday, April 22, 2012
SICP 2.56 - 2.58: Symbolic Differentiation
From SICP section 2.3.2 Example: Symbolic Differentiation
This section of SICP presents an application of symbol manipulation in the form of the following procedure that performs symbolic differentiation of algebraic expressions.
The following supporting procedures are required by deriv. Each one is explained in the text.
With these definitions, we can perform differentiation on algebraic expressions in Scheme's familiar prefix notation.
This procedure returns results that are correct, but the expressions are not in their simplest form. For example, instead of (+ 1 0) we'd like the procedure to simplify the expression to 1. Similarly, the expression (+ (* x 0) (* 1 y)) can be simplified to y. We only need to change the constructors make-sum and make-product to simplify the resulting expressions. We can change make-sum so that if both its arguments are numbers, make-sum will return their sum. Also, if either of the arguments is 0, then make-sum will return the other summand (whether it's a number or a symbol).
Similarly, make-product should return 0 if either of its arguments is 0, and if either of its arguments is 1 it should return the other argument.
Both of these new implementations make use of the =number? procedure to check whether an expression is equal to an expected value.
Here's how the improved procedures work with the same three examples.
The first two resulting expressions are now in simplest form. The third is greatly improved, but could still be better.
Exercise 2.56 asks us to extend the deriv procedure to handle more kinds of expressions. We're to implement the differentiation rule
by adding a new clause to the deriv program and defining appropriate procedures exponentiation?, base, exponent, and make-exponentiation. (We'll use the symbol ** to denote exponentiation.) We'll also build in the rules that anything raised to the power 0 is 1 and any expression raised to the power 1 is the expression itself. We can base the implementations of exponentiation?, base, and exponent on the corresponding procedures used for sums and products.
Similarly, our implementation of make-exponentiation will be based on the updated versions of make-sum and make-product, since we're going to build in two rules of exponentiation that will simplify resulting expressions.
The last step before testing is to extend the deriv procedure itself to recognize and handle exponentiation.
We can test the extended implementation of deriv using an example from the beginning of the current section of the text. "For example, if the arguments to the procedure are $ax^2 + bx + c$ and x, the procedure should return $2ax + b$." I'll translate the expression to prefix notation in multiple steps so we can see the effect that each term has on the result.
Exercise 2.57 asks us to extend the deriv program to handle sums and products with arbitrary numbers of (two or more) terms. The third example above could be expressed as
We'll do this by changing only the representation for sums and products, without changing the deriv procedure itself. (For example, the addend of a sum would be the first term, and the augend would be the sum of the rest of the terms.) We can change the representation for sums and products by changing only two procedures, augend and multiplicand. The original implementations of these procedures simply returned the second argument in a sum or product, respectively. Instead of returning a single value or symbol, we'll need to modify these procedures so they can return an expression.
The new augend procedure first tests to see if the expression passed in has only two arguments by checking to see if its third argument is null. If the expression has only two arguments, the second one is returned, just as it would have been in the original implementation. Otherwise, if the expression has more than two arguments, all of the arguments following the first one are returned in a new sum expresssion. The new implementation of multiplicand is pretty much the same.
We can use the example from the text to test that the deriv procedure works correctly with the new representations of sums and products.
Exercise 2.58 asks us to modify the differentiation program so that it works with ordinary mathematical notation (where + and * are infix rather than prefix operators). Since the differentiation program is defined in terms of abstract data, we can modify it to work with different representations of expressions solely by changing the predicates, selectors, and constructors that define the representation of the algebraic expressions on which the differentiator is to operate. We're to do this in two steps, a fully parenthesized version and a version that drops unnecessary parentheses:
a. Show how to do this in order to differentiate algebraic expressions presented in infix form, such as (x + (3 * (x + (y + 2)))). To simplify the task, assume that + and * always take two arguments and that expressions are fully parenthesized.
We can solve the first part of the problem simply by changing the procedures that define how a sum is represented. Instead of the + symbol appearing first in an expression, it will now appear second.
The definitions for products are equivalent.
We can test with a few simple examples before moving to the more complicated example given in the text.
b. The problem becomes substantially harder if we allow standard algebraic notation, such as (x + 3 * (x + y + 2)), which drops unnecessary parentheses and assumes that multiplication is done before addition. Can you design appropriate predicates, selectors, and constructors for this notation such that our derivative program still works?
Only a few additional changes are necessary in order to correctly interpret expressions where unnecessary parentheses are excluded. In part a above we defined both the augend and multiplicand of an expression using caddr. We were able to do this because we knew all expressions would be two parameters separated by an operator, and that the expression would be contained in parentheses.
Since this is no longer the case, we now want the augend and multiplicand procedures to return an entire subexpression, so we'd like to use cddr. The only problem with this is that cddr always returns a list, so it will fail in those cases where the augend or multiplicand is a single value or symbol, as would be the case in fully-parenthesized expressions. We can get around this limitation by introducing a procedure that will simplify sub-expressions of this form by returning a single value or symbol if that's all there is to an expression.
Now we can define augend and multiplicand in terms of simplify and cddr.
We can test a few different expressions, starting with the example given.
Finally, we should also test a few simpler cases to make sure our changes didn't break anything.
Related:
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
This section of SICP presents an application of symbol manipulation in the form of the following procedure that performs symbolic differentiation of algebraic expressions.
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp)
(if (same-variable? exp var) 1 0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else
(error "unknown expression type -- DERIV" exp))))
The following supporting procedures are required by deriv. Each one is explained in the text.
(define (variable? x) (symbol? x)) (define (same-variable? v1 v2) (and (variable? v1) (variable? v2) (eq? v1 v2))) (define (make-sum a1 a2) (list '+ a1 a2)) (define (make-product m1 m2) (list '* m1 m2)) (define (sum? x) (and (pair? x) (eq? (car x) '+))) (define (addend s) (cadr s)) (define (augend s) (caddr s)) (define (product? x) (and (pair? x) (eq? (car x) '*))) (define (multiplier p) (cadr p)) (define (multiplicand p) (caddr p))
With these definitions, we can perform differentiation on algebraic expressions in Scheme's familiar prefix notation.
> (deriv '(+ x 3) 'x) (+ 1 0) > (deriv '(* x y) 'x) (+ (* x 0) (* 1 y)) > (deriv '(* (* x y) (+ x 3)) 'x) (+ (* (* x y) (+ 1 0)) (* (+ (* x 0) (* 1 y)) (+ x 3)))
This procedure returns results that are correct, but the expressions are not in their simplest form. For example, instead of (+ 1 0) we'd like the procedure to simplify the expression to 1. Similarly, the expression (+ (* x 0) (* 1 y)) can be simplified to y. We only need to change the constructors make-sum and make-product to simplify the resulting expressions. We can change make-sum so that if both its arguments are numbers, make-sum will return their sum. Also, if either of the arguments is 0, then make-sum will return the other summand (whether it's a number or a symbol).
(define (make-sum a1 a2)
(cond ((=number? a1 0) a2)
((=number? a2 0) a1)
((and (number? a1) (number? a2)) (+ a1 a2))
(else (list '+ a1 a2))))
Similarly, make-product should return 0 if either of its arguments is 0, and if either of its arguments is 1 it should return the other argument.
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (list '* m1 m2))))
Both of these new implementations make use of the =number? procedure to check whether an expression is equal to an expected value.
(define (=number? exp num) (and (number? exp) (= exp num)))
Here's how the improved procedures work with the same three examples.
> (deriv '(+ x 3) 'x) 1 > (deriv '(* x y) 'x) y > (deriv '(* (* x y) (+ x 3)) 'x) (+ (* x y) (* y (+ x 3)))
The first two resulting expressions are now in simplest form. The third is greatly improved, but could still be better.
Exercise 2.56 asks us to extend the deriv procedure to handle more kinds of expressions. We're to implement the differentiation rule
$\frac{d(u^n)}{dx} = nu^{(n-1)} (\frac{du}{dx})$
by adding a new clause to the deriv program and defining appropriate procedures exponentiation?, base, exponent, and make-exponentiation. (We'll use the symbol ** to denote exponentiation.) We'll also build in the rules that anything raised to the power 0 is 1 and any expression raised to the power 1 is the expression itself. We can base the implementations of exponentiation?, base, and exponent on the corresponding procedures used for sums and products.
(define (exponentiation? x) (and (pair? x) (eq? (car x) '**))) (define (base e) (cadr e)) (define (exponent e) (caddr e))
Similarly, our implementation of make-exponentiation will be based on the updated versions of make-sum and make-product, since we're going to build in two rules of exponentiation that will simplify resulting expressions.
(define (make-exponentiation base exponent)
(cond ((=number? exponent 0) 1)
((=number? exponent 1) base)
((and (number? base) (number? exponent)) (expt base exponent))
(else (list '** base exponent))))
The last step before testing is to extend the deriv procedure itself to recognize and handle exponentiation.
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp)
(if (same-variable? exp var) 1 0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
((exponentiation? exp)
(make-product
(make-product (exponent exp)
(make-exponentiation
(base exp)
(make-sum (exponent exp) -1)))
(deriv (base exp) var)))
(else
(error "unknown expression type -- DERIV" exp))))
We can test the extended implementation of deriv using an example from the beginning of the current section of the text. "For example, if the arguments to the procedure are $ax^2 + bx + c$ and x, the procedure should return $2ax + b$." I'll translate the expression to prefix notation in multiple steps so we can see the effect that each term has on the result.
> (deriv '(** x 2) 'x) (* 2 x) > (deriv '(* a (** x 2)) 'x) (* a (* 2 x)) > (deriv '(+ (* a (** x 2)) (* b x)) 'x) (+ (* a (* 2 x)) b) > (deriv '(+ (+ (* a (** x 2)) (* b x)) c) 'x) (+ (* a (* 2 x)) b)
Exercise 2.57 asks us to extend the deriv program to handle sums and products with arbitrary numbers of (two or more) terms. The third example above could be expressed as
(deriv '(* x y (+ x 3)) 'x)
We'll do this by changing only the representation for sums and products, without changing the deriv procedure itself. (For example, the addend of a sum would be the first term, and the augend would be the sum of the rest of the terms.) We can change the representation for sums and products by changing only two procedures, augend and multiplicand. The original implementations of these procedures simply returned the second argument in a sum or product, respectively. Instead of returning a single value or symbol, we'll need to modify these procedures so they can return an expression.
(define (augend s)
(if (null? (cdddr s))
(caddr s)
(cons '+ (cddr s))))
The new augend procedure first tests to see if the expression passed in has only two arguments by checking to see if its third argument is null. If the expression has only two arguments, the second one is returned, just as it would have been in the original implementation. Otherwise, if the expression has more than two arguments, all of the arguments following the first one are returned in a new sum expresssion. The new implementation of multiplicand is pretty much the same.
(define (multiplicand p)
(if (null? (cdddr p))
(caddr p)
(cons '* (cddr p))))
We can use the example from the text to test that the deriv procedure works correctly with the new representations of sums and products.
> (deriv '(* x y (+ x 3)) 'x) (+ (* x y) (* y (+ x 3)))
Exercise 2.58 asks us to modify the differentiation program so that it works with ordinary mathematical notation (where + and * are infix rather than prefix operators). Since the differentiation program is defined in terms of abstract data, we can modify it to work with different representations of expressions solely by changing the predicates, selectors, and constructors that define the representation of the algebraic expressions on which the differentiator is to operate. We're to do this in two steps, a fully parenthesized version and a version that drops unnecessary parentheses:
a. Show how to do this in order to differentiate algebraic expressions presented in infix form, such as (x + (3 * (x + (y + 2)))). To simplify the task, assume that + and * always take two arguments and that expressions are fully parenthesized.
We can solve the first part of the problem simply by changing the procedures that define how a sum is represented. Instead of the + symbol appearing first in an expression, it will now appear second.
(define (make-sum a1 a2)
(cond ((=number? a1 0) a2)
((=number? a2 0) a1)
((and (number? a1) (number? a2)) (+ a1 a2))
(else (list a1 '+ a2))))
(define (sum? x)
(and (pair? x) (eq? (cadr x) '+)))
(define (addend s) (car s))
(define (augend s) (caddr s))
The definitions for products are equivalent.
(define (make-product m1 m2)
(cond ((or (=number? m1 0) (=number? m2 0)) 0)
((=number? m1 1) m2)
((=number? m2 1) m1)
((and (number? m1) (number? m2)) (* m1 m2))
(else (list m1 '* m2))))
(define (product? x)
(and (pair? x) (eq? (cadr x) '*)))
(define (multiplier p) (car p))
(define (multiplicand p) (caddr p))
We can test with a few simple examples before moving to the more complicated example given in the text.
> (deriv '(x + 3) 'x) 1 > (deriv '(x * y) 'x) y > (deriv '(x + (3 * (x + (y + 2)))) 'x) 4
b. The problem becomes substantially harder if we allow standard algebraic notation, such as (x + 3 * (x + y + 2)), which drops unnecessary parentheses and assumes that multiplication is done before addition. Can you design appropriate predicates, selectors, and constructors for this notation such that our derivative program still works?
Only a few additional changes are necessary in order to correctly interpret expressions where unnecessary parentheses are excluded. In part a above we defined both the augend and multiplicand of an expression using caddr. We were able to do this because we knew all expressions would be two parameters separated by an operator, and that the expression would be contained in parentheses.
Since this is no longer the case, we now want the augend and multiplicand procedures to return an entire subexpression, so we'd like to use cddr. The only problem with this is that cddr always returns a list, so it will fail in those cases where the augend or multiplicand is a single value or symbol, as would be the case in fully-parenthesized expressions. We can get around this limitation by introducing a procedure that will simplify sub-expressions of this form by returning a single value or symbol if that's all there is to an expression.
(define (simplify exp) (if (null? (cdr exp)) (car exp) exp))
Now we can define augend and multiplicand in terms of simplify and cddr.
(define (augend s) (simplify (cddr s))) (define (multiplicand p) (simplify (cddr p)))
We can test a few different expressions, starting with the example given.
> (deriv '(x + 3 * (x + y + 2)) 'x) 4 > (deriv '(x + 3 * (x + y + 2)) 'y) 3
Finally, we should also test a few simpler cases to make sure our changes didn't break anything.
> (deriv '(x + 3) 'x) 1 > (deriv '(x * y) 'x) y > (deriv '(x * y * (x + 3)) 'x) ((x * y) + (y * (x + 3)))
Related:
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
Labels:
calculus,
derivative,
learning,
math,
programming,
scheme,
sicp
Thursday, March 1, 2012
SICP 2.53 - 2.55: Symbolic Data
From SICP section 2.3.1 Quotation
This section of SICP introduces quotation, which gives us the ability to manipulate symbols as well as data values. When we quote a symbol the interpreter returns the literal symbol instead of the value that the symbol points to.
As a shorthand for
We can also use quotation with compound objects.
Finally, we're introduced to the primitive
Exercise 2.53 asks us what the interpreter would print in response to evaluating each of the following expressions? See if you can predict what the output should be before trying each expression.
The first expression just creates a list containing three symbols, so it should evaluate the same as
The second expression creates a list that contains a list that contains a symbol.
The third expression gets the
The fourth expression gets the second element of the same list as above.
The fifth expression is checking to see if the
The sixth expression is using the
The final expression is also using
Exercise 2.54 asks us to define a procedure
The procedure starts by checking to see if both parameters are null and returns
Exercise 2.55 asks us to explain why when a user types the expression
the interpreter prints back
Remember that
The sub-expression
Related:
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
This section of SICP introduces quotation, which gives us the ability to manipulate symbols as well as data values. When we quote a symbol the interpreter returns the literal symbol instead of the value that the symbol points to.
> (define a 1)
> a
1
> (quote a)
a
As a shorthand for
quote we can place a single quote symbol at the beginning of the object to be quoted.> 'a
a
We can also use quotation with compound objects.
> (define x '(a b c))
> x
(a b c)
> (car x)
a
Finally, we're introduced to the primitive
eq?, which takes two symbols as arguments and tests whether they are the same (they consist of the same characters in the same order). We're also shown how we can use eq? to create a procedure memq that takes two arguments, a symbol and a list. If the symbol is not contained in the list, then memq returns false. Otherwise, it returns the sub-list that begins with the first occurrence of the symbol.Exercise 2.53 asks us what the interpreter would print in response to evaluating each of the following expressions? See if you can predict what the output should be before trying each expression.
(list 'a 'b 'c)
(list (list 'george))
(cdr '((x1 x2) (y1 y2)))
(cadr '((x1 x2) (y1 y2)))
(pair? (car '(a short list)))
(memq 'red '((red shoes) (blue socks)))
(memq 'red '(red shoes blue socks))
The first expression just creates a list containing three symbols, so it should evaluate the same as
'(a b c).> '(a b c)
(a b c)
> (list 'a 'b 'c)
(a b c)
The second expression creates a list that contains a list that contains a symbol.
> (list (list 'george))
((george))
The third expression gets the
cdr of a list containing two lists of symbols. Remember from earlier sections that the car of a list is the first element in a list and the cdr is the remainder of the list.> (cdr '((x1 x2) (y1 y2)))
((y1 y2))
The fourth expression gets the second element of the same list as above.
> (cadr '((x1 x2) (y1 y2)))
(y1 y2)
The fifth expression is checking to see if the
car of a quoted list is a pair. You should be able to see that it's not, but try evaluating sub-expressions if you're unsure.> '(a short list)
(a short list)
> (car '(a short list))
a
> (pair? (car '(a short list)))
#f
The sixth expression is using the
memq procedure to see if a symbol is contained in a list. Remember that memq only checks the highest-level elements of the list, it doesn't recursively look inside any sub-lists.> (memq 'red '((red shoes) (blue socks)))
#f
The final expression is also using
memq to look for a symbol in a list, but this time with different results.> (memq 'red '(red shoes blue socks))
(red shoes blue socks)
Exercise 2.54 asks us to define a procedure
equal? that takes two parameters and returns true if they contain equal elements arranged in the same order. The parameters can be values, symbols, lists of symbols, or lists containing both symbols and nested lists. We are to define equal? recursively in terms of the basic eq? equality of symbols.(define (equal? p1 p2)
(cond ((and (null? p1) (null? p2)) #t)
((or (null? p1) (null? p2)) #f)
((and (pair? p1) (pair? p2))
(and (equal? (car p1) (car p2))
(equal? (cdr p1) (cdr p2))))
((or (pair? p1) (pair? p2)) #f)
(else (eq? p1 p2))))
The procedure starts by checking to see if both parameters are null and returns
#t if they are. It then checks to see if only one parameter but not the other is null. Next it checks to see if both parameters are pairs, and if they are it recursively checks to see if they have the same car and the same cdr. Next it checks to see if only one of the parameters is a pair and returns #f if that's the case. Finally, it checks to see if the two parameters are the same symbol or have the same value. We can run several tests to validate all the cases above.> (equal? '() '())
#t
> (equal? '() 'a)
#f
> (equal? '((x1 x2) (y1 y2)) '((x1 x2) (y1 y2)))
#t
> (equal? '((x1 x2) (y1 y2)) '((x1 x2 x3) (y1 y2)))
#f
> (equal? '(x1 x2) 'y1)
#f
> (equal? 'abc 'abc)
#t
> (equal? 123 123)
#t
Exercise 2.55 asks us to explain why when a user types the expression
(car ''abracadabra)
the interpreter prints back
quote.Remember that
' is just shorthand for quote, so the expression above is equivalent to(car (quote (quote abracadabra)))
The sub-expression
(quote (quote abracadabra)) is equivalent to '(quote abracadabra), which is just the list containing the two symbols quote and abracadabra, making the car of that list simply the symbol quote.Related:
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
Labels:
learning,
programming,
scheme,
sicp
Sunday, February 5, 2012
SICP 2.52: Levels of Language for Robust Design
From SICP section 2.2.4 Example: A Picture Language
Just as we did in previous exercises, we can use the PLT Scheme SICP Picture Language package to run the solutions to the following exercises. You can load the picture package by putting the following
Exercise 2.52 asks us to make changes to the square limit of
2.52a. Add some segments to the primitive
This change requires that we make a change at a low level of abstraction, in adding segments to the
2.52b. Change the pattern constructed by
For this requirement we need to work in the middle layer of abstraction. To use only one copy of the

2.52c. Modify the version of
We're not using the Mr. Rogers painter from the text, but we can still rearrange the

Related:
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
Just as we did in previous exercises, we can use the PLT Scheme SICP Picture Language package to run the solutions to the following exercises. You can load the picture package by putting the following
(require...) expression at the beginning of your Scheme file.(require (planet "sicp.ss" ("soegaard" "sicp.plt" 2 1)))Exercise 2.52 asks us to make changes to the square limit of
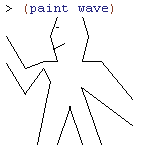
wave shown in figure 2.9 by working at the appropriate level of abstraction for the required change. (We'll need all the code we wrote in exercises 2.44 and 2.49 to start out with, so copy those into a new Scheme file.)2.52a. Add some segments to the primitive
wave painter of exercise 2.49 (to add a smile, for example).This change requires that we make a change at a low level of abstraction, in adding segments to the
wave painter itself. Let's add an eye and a smiling mouth on the left side of the head so it looks like the person in wave is looking in that direction.; The wave painter (2.49d).
; Add some segments to form a smile (2.52a)
(define wave-segments
(list
(make-segment
(make-vect 0.006 0.840)
(make-vect 0.155 0.591))
(make-segment
(make-vect 0.006 0.635)
(make-vect 0.155 0.392))
(make-segment
(make-vect 0.304 0.646)
(make-vect 0.155 0.591))
(make-segment
(make-vect 0.298 0.591)
(make-vect 0.155 0.392))
(make-segment
(make-vect 0.304 0.646)
(make-vect 0.403 0.646))
(make-segment
(make-vect 0.298 0.591)
(make-vect 0.354 0.492))
(make-segment ; left face
(make-vect 0.403 0.646)
(make-vect 0.348 0.845))
(make-segment
(make-vect 0.354 0.492)
(make-vect 0.249 0.000))
(make-segment
(make-vect 0.403 0.000)
(make-vect 0.502 0.293))
(make-segment
(make-vect 0.502 0.293)
(make-vect 0.602 0.000))
(make-segment
(make-vect 0.348 0.845)
(make-vect 0.403 0.999))
(make-segment
(make-vect 0.602 0.999)
(make-vect 0.652 0.845))
(make-segment
(make-vect 0.652 0.845)
(make-vect 0.602 0.646))
(make-segment
(make-vect 0.602 0.646)
(make-vect 0.751 0.646))
(make-segment
(make-vect 0.751 0.646)
(make-vect 0.999 0.343))
(make-segment
(make-vect 0.751 0.000)
(make-vect 0.597 0.442))
(make-segment
(make-vect 0.597 0.442)
(make-vect 0.999 0.144))
(make-segment ; eye
(make-vect 0.395 0.916)
(make-vect 0.410 0.916))
(make-segment ; smile
(make-vect 0.376 0.746)
(make-vect 0.460 0.790))))

2.52b. Change the pattern constructed by
corner-split (for example, by using only one copy of the up-split and right-split images instead of two).For this requirement we need to work in the middle layer of abstraction. To use only one copy of the
up-split and right-split images instead of two, we can simply remove the references to top-left and bottom-right that appear in the original implementation of corner-split.(define (corner-split painter n)
(if (= n 0)
painter
(let ((up (up-split painter (- n 1)))
(right (right-split painter (- n 1)))
(corner (corner-split painter (- n 1))))
(beside (below painter up)
(below right corner)))))

2.52c. Modify the version of
square-limit that uses square-of-four so as to assemble the corners in a different pattern. (For example, you might make the big Mr. Rogers look outward from each corner of the square.)We're not using the Mr. Rogers painter from the text, but we can still rearrange the
square-limit painter so that the largest wave image is drawn in the four corners by simply rotating the corner-split painter by 180 degrees.(define (square-limit painter n)
(let ((quarter (rotate180 (corner-split painter n))))
(let ((half (beside (flip-horiz quarter) quarter)))
(below (flip-vert half) half))))

Related:
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
Labels:
learning,
programming,
scheme,
sicp
Monday, January 2, 2012
SICP 2.50 - 2.51: Transforming and Combining Painters
From SICP section 2.2.4 Example: A Picture Language
Just as we did in exercises 2.44, 2.45, and 2.49, we can use the PLT Scheme SICP Picture Language package to run the solutions to the following exercises. You can load the picture package by putting the following
Exercise 2.50 asks us to define the transformation
We're expected to use the
For example, instead of defining
We would instead pass the painter as an argument to the procedure returned from
The arguments to
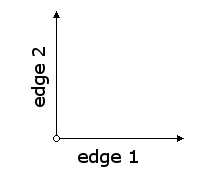
These edges are defined by the points (0, 0) for the origin, (1, 0) for the end point of the first edge, and (0, 1) for the end point of the second edge. In order to transform a painter we just need to redraw the figure above in the desired orientation, then call transform-painter with the new positions of the origin and the end points of the edges.
To flip a painter horizontally we just move the origin and left edge to the right.
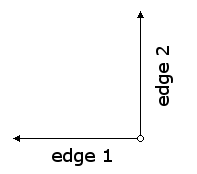
This gives the bottom edge a new endpoint as well. The procedure (based on
The following images show the locations of the origin and edges when we rotate an image counterclockwise by 180 and 270 degrees.
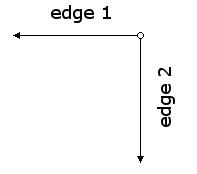
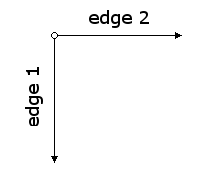
We can implement the procedures using the origin and endpoints shown in the figures above.
Use the

Exercise 2.51 asks us to define the
Translating the
The
We need to redefine the
The second implementation of
Once again, we can test with

Related:
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
Just as we did in exercises 2.44, 2.45, and 2.49, we can use the PLT Scheme SICP Picture Language package to run the solutions to the following exercises. You can load the picture package by putting the following
(require...) expression at the beginning of your Scheme file.(require (planet "sicp.ss" ("soegaard" "sicp.plt" 2 1)))Exercise 2.50 asks us to define the transformation
flip-horiz, which flips painters horizontally, and transformations that rotate painters counterclockwise by 180 degrees and 270 degrees.We're expected to use the
transform-painter procedure defined earlier in section 2.2.4 of the text. Since we're using the PLT Scheme SICP Picture Language package, we'll be using a version of transform-painter that's defined slightly differently than the one in the text. This procedure does not take the painter to be transformed as an argument, as does the version given in the text. Instead it takes the points that specify the corners of the new frame as arguments and returns a procedure that takes the painter as its argument.For example, instead of defining
flip-vert as:(define (flip-vert painter)
(transform-painter painter
(make-vect 0.0 1.0) ; new origin
(make-vect 1.0 1.0) ; new end of edge1
(make-vect 0.0 0.0))) ; new end of edge2
We would instead pass the painter as an argument to the procedure returned from
transform-painter as follows:(define (flip-vertical painter)
((transform-painter (make-vect 0.0 1.0)
(make-vect 1.0 1.0)
(make-vect 0.0 0.0))
painter))
The arguments to
transform-painter are points (represented as vectors) that specify the corners of the new frame. The first point specifies the new frame's origin and the other two specify the ends of its edge vectors. Remember that the origin point in a frame is normally in the lower left hand corner. The first edge vector is the bottom edge of frame and the second edge vector is the left edge of the frame.
These edges are defined by the points (0, 0) for the origin, (1, 0) for the end point of the first edge, and (0, 1) for the end point of the second edge. In order to transform a painter we just need to redraw the figure above in the desired orientation, then call transform-painter with the new positions of the origin and the end points of the edges.
To flip a painter horizontally we just move the origin and left edge to the right.

This gives the bottom edge a new endpoint as well. The procedure (based on
flip-vert) would be:(define (flip-horizontal painter)
((transform-painter (make-vect 1.0 0.0) ; origin
(make-vect 0.0 0.0) ; corner1
(make-vect 1.0 1.0)) ; corner2
painter))
The following images show the locations of the origin and edges when we rotate an image counterclockwise by 180 and 270 degrees.


We can implement the procedures using the origin and endpoints shown in the figures above.
(define (rotate-180 painter)
((transform-painter (make-vect 1.0 1.0)
(make-vect 0.0 1.0)
(make-vect 1.0 0.0))
painter))
(define (rotate-270 painter)
((transform-painter (make-vect 0.0 1.0)
(make-vect 0.0 0.0)
(make-vect 1.0 1.0))
painter))
Use the
einstein painter provided by the PLT Scheme SICP Picture Language package to check the output of the procedures above.
Exercise 2.51 asks us to define the
below operation for painters. The below procedure takes two painters as arguments. The resulting painter draws the first painter in the bottom of the frame and the second painter in the top. We're asked to define below in two different ways -- first by writing a procedure that is analogous to the beside procedure given in the text, and again in terms of beside and suitable rotation operations like the ones we defined in exercise 2.50.Translating the
beside procedure from the text to create the first below procedure is a simple matter of applying what we learned in exercise 2.50 above.(define (beside painter1 painter2)
(let ((split-point (make-vect 0.5 0.0)))
(let ((paint-left
(transform-painter painter1
(make-vect 0.0 0.0)
split-point
(make-vect 0.0 1.0)))
(paint-right
(transform-painter painter2
split-point
(make-vect 1.0 0.0)
(make-vect 0.5 1.0))))
(lambda (frame)
(paint-left frame)
(paint-right frame)))))
The
beside procedure first defines a split-point at the bottom center of the frame that splits the frame vertically. It then transforms the two painters provided so that they each fit into one half of the frame. Finally, it returns a procedure that, when given a frame, paints the two images in the left and right halves of the frame. Here's the analogous below procedure:; 2.51a
(define (below-a painter1 painter2)
(let ((split-point (make-vect 0.0 0.5)))
(let ((paint-bottom
((transform-painter (make-vect 0.0 0.0)
(make-vect 1.0 0.0)
split-point)
painter1))
(paint-top
((transform-painter split-point
(make-vect 1.0 0.5)
(make-vect 0.0 1.0))
painter2)))
(lambda (frame)
(paint-bottom frame)
(paint-top frame)))))
We need to redefine the
split-point so that it divides the frame horizontally instead of vertically. We then transform the painters so that they fit into the bottom and top halves of the frame. Finally, we return a procedure that draws the two halves.The second implementation of
below is even simpler than the first. We just need to draw the two painters beside each other then rotate the frame by 90 degrees. When we do that the two images will be draw on their side, so we need to rotate the individual images 90 degrees in the opposite direction inside their smaller frames. This is equivalent to rotating them 270 degrees in the same direction.; 2.51b
(define (rotate-90 painter)
((transform-painter (make-vect 1.0 0.0)
(make-vect 1.0 1.0)
(make-vect 0.0 0.0))
painter))
(define (below-b painter1 painter2)
(rotate-90 (beside (rotate-270 painter1) (rotate-270 painter2))))
Once again, we can test with
einstein to verify that these two procedures both give us the desired output.
Related:
For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.
Labels:
learning,
programming,
scheme,
sicp
Subscribe to:
Comments (Atom)
