SICP 2.50 - 2.51: Transforming and Combining Painters

From SICP section 2.2.4 Example: A Picture Language

Just as we did in exercises 2.44, 2.45, and 2.49, we can use the PLT Scheme SICP Picture Language package to run the solutions to the following exercises. You can load the picture package by putting the following (require...) expression at the beginning of your Scheme file.

(require (planet "sicp.ss" ("soegaard" "sicp.plt" 2 1)))

Exercise 2.50 asks us to define the transformation flip-horiz, which flips painters horizontally, and transformations that rotate painters counterclockwise by 180 degrees and 270 degrees.

We're expected to use the transform-painter procedure defined earlier in section 2.2.4 of the text. Since we're using the PLT Scheme SICP Picture Language package, we'll be using a version of transform-painter that's defined slightly differently than the one in the text. This procedure does not take the painter to be transformed as an argument, as does the version given in the text. Instead it takes the points that specify the corners of the new frame as arguments and returns a procedure that takes the painter as its argument.

For example, instead of defining flip-vert as:

(define (flip-vert painter)
   (transform-painter painter
             (make-vect 0.0 1.0)   ; new origin
             (make-vect 1.0 1.0)   ; new end of edge1
             (make-vect 0.0 0.0))) ; new end of edge2

We would instead pass the painter as an argument to the procedure returned from transform-painter as follows:

(define (flip-vertical painter)
   ((transform-painter (make-vect 0.0 1.0)
                       (make-vect 1.0 1.0)
                       (make-vect 0.0 0.0))
    painter))

The arguments to transform-painter are points (represented as vectors) that specify the corners of the new frame. The first point specifies the new frame's origin and the other two specify the ends of its edge vectors. Remember that the origin point in a frame is normally in the lower left hand corner. The first edge vector is the bottom edge of frame and the second edge vector is the left edge of the frame.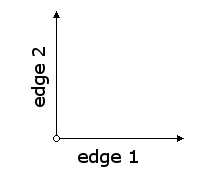



These edges are defined by the points (0, 0) for the origin, (1, 0) for the end point of the first edge, and (0, 1) for the end point of the second edge. In order to transform a painter we just need to redraw the figure above in the desired orientation, then call transform-painter with the new positions of the origin and the end points of the edges.

To flip a painter horizontally we just move the origin and left edge to the right.



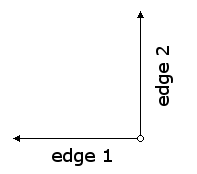
This gives the bottom edge a new endpoint as well. The procedure (based on flip-vert) would be:

(define (flip-horizontal painter)
   ((transform-painter (make-vect 1.0 0.0)   ; origin
                       (make-vect 0.0 0.0)   ; corner1
                       (make-vect 1.0 1.0))  ; corner2
    painter))

The following images show the locations of the origin and edges when we rotate an image counterclockwise by 180 and 270 degrees.





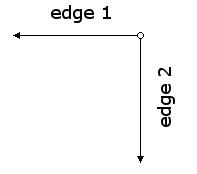
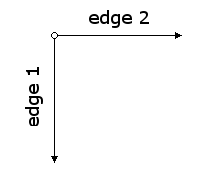
We can implement the procedures using the origin and endpoints shown in the figures above.

(define (rotate-180 painter)
   ((transform-painter (make-vect 1.0 1.0)
                       (make-vect 0.0 1.0)
                       (make-vect 1.0 0.0))
    painter))

(define (rotate-270 painter)
   ((transform-painter (make-vect 0.0 1.0)
                       (make-vect 0.0 0.0)
                       (make-vect 1.0 1.0))
    painter))

Use the einstein painter provided by the PLT Scheme SICP Picture Language package to check the output of the procedures above.




Exercise 2.51 asks us to define the below operation for painters. The below procedure takes two painters as arguments. The resulting painter draws the first painter in the bottom of the frame and the second painter in the top. We're asked to define below in two different ways -- first by writing a procedure that is analogous to the beside procedure given in the text, and again in terms of beside and suitable rotation operations like the ones we defined in exercise 2.50.

Translating the beside procedure from the text to create the first below procedure is a simple matter of applying what we learned in exercise 2.50 above.

(define (beside painter1 painter2)
   (let ((split-point (make-vect 0.5 0.0)))
   (let ((paint-left
         (transform-painter painter1
                            (make-vect 0.0 0.0)
                            split-point
                            (make-vect 0.0 1.0)))
         (paint-right
         (transform-painter painter2
                            split-point
                           (make-vect 1.0 0.0)
                           (make-vect 0.5 1.0))))
   (lambda (frame)
     (paint-left frame)
     (paint-right frame)))))

The beside procedure first defines a split-point at the bottom center of the frame that splits the frame vertically. It then transforms the two painters provided so that they each fit into one half of the frame. Finally, it returns a procedure that, when given a frame, paints the two images in the left and right halves of the frame. Here's the analogous below procedure:

; 2.51a
(define (below-a painter1 painter2)
   (let ((split-point (make-vect 0.0 0.5)))
   (let ((paint-bottom
        ((transform-painter (make-vect 0.0 0.0)
                            (make-vect 1.0 0.0)
                            split-point)
         painter1))
        (paint-top
        ((transform-painter split-point
                            (make-vect 1.0 0.5)
                            (make-vect 0.0 1.0))
         painter2)))
   (lambda (frame)
     (paint-bottom frame)
     (paint-top frame)))))

We need to redefine the split-point so that it divides the frame horizontally instead of vertically. We then transform the painters so that they fit into the bottom and top halves of the frame. Finally, we return a procedure that draws the two halves.

The second implementation of below is even simpler than the first. We just need to draw the two painters beside each other then rotate the frame by 90 degrees. When we do that the two images will be draw on their side, so we need to rotate the individual images 90 degrees in the opposite direction inside their smaller frames. This is equivalent to rotating them 270 degrees in the same direction.

; 2.51b
(define (rotate-90 painter)
 ((transform-painter (make-vect 1.0 0.0)
                     (make-vect 1.0 1.0)
                     (make-vect 0.0 0.0))
   painter))

(define (below-b painter1 painter2)
   (rotate-90 (beside (rotate-270 painter1) (rotate-270 painter2))))

Once again, we can test with einstein to verify that these two procedures both give us the desired output.




Related:

For links to all of the SICP lecture notes and exercises that I've done so far, see The SICP Challenge.