Number System

In a slightly eccentric numbering system, the numbers on the left are converted to regular decimal numbers by applying a simple rule.

9999 = 4
8888 = 8
1816 = 3
1212 = 0

Can you answer

2419 = ?

Click below for the answer.

To convert numbers from this system to decimal, just count the number of closed areas in each digit. The digit 9 has one closed area, so 9999 = 4. An 8 has two closed areas, so 8888 = 8, and so on. The digits in 2419 have two closed areas, so 2419 = 2.

Fraction of 1000

What is 1/2 of 2/3 of 3/4 of 4/5 of 5/6 of 6/7 of 7/8 of 8/9 of 9/10 of 1000? Click below for the answer.

At first glance, this problem looks a lot harder than it is. If you work backwards starting at 9/10 of 1000, it's easier to see that the final answer is 100.

Three Water Bottles

You have three water bottles with capacities of 8 quarts, 5 quarts, and 3 quarts. The largest bottle is filled with water, and the other two are empty. If there are no graduation marks on any of the bottles, how can you split the water evenly so that two of the bottles contain exactly 4 quarts each? You can only use these three bottles. Click below for the answer.

There may be other ways to solve this problem, but here's one sequence that works.

1. Fill the 5 quart bottle, leaving 3 quarts in the 8 quart bottle.
2. Pour 3 quarts from the 5 quart bottle into the 3 quart bottle, leaving 2 quarts in the 5 quart bottle.
3. Empty the 3 quart bottle into the 8 quart bottle , leaving 6 quarts in the 8 quart bottle.
4. Pour the 2 quarts from the 5 quart bottle into the 3 quart bottle.
5. Fill the 5 quart bottle from the 8 quart bottle , leaving 1 quart in the 8 quart bottle.
6. Pour 1 quart from the 5 quart bottle into the 3 quart bottle (filling it), leaving 4 quarts in the 5 quart bottle.
7. Pour the 3 quarts from the 3 quart bottle into the 8 quart bottle, leaving 4 quarts in the 8 quart bottle.

That's a lot to follow, so here are the steps in tabular form.

8 qt.	5 qt.	3 qt.
8	0	0
3	5	0
3	2	3
6	2	0
6	0	2
1	5	2
1	4	3
4	4	0

The Compulsive Gambler

You are approached by a compulsive gambler with the following proposal. You are to flip a fair coin four times. If heads and tails both appear twice each, he will pay you $11. If any other combination of heads and tails appears, you have to pay him only $10. Do you take the wager? Click below for the answer.

This is not a good gamble. Below are all the possible outcomes for four successive coin flips.

Notice that exactly two heads and two tails only appear six out of sixteen times, so you can only expect to win this game about 37.5% of the time. At the offered stakes ($11 for a win, $10 for a loss) you'd be losing an average of around $2.12 every time you play.

This problem appeared as an exercise in Introductory Graph Theory by Gary Chartrand.
See my Probability GitHub repository for a script that shows how to model this problem in Python.

The Lily Pad

A lily pad starts out very small, but doubles in size every day. After 60 days it has completely covered a pond. After how many days had it covered one-quarter the area of the pond? Click below for the answer.

The instinctive answer might seem to be 15 days, but that would only be correct if the lily pad was growing linearly. Remember, the lily pad doubles in size every day, which is exponential. To solve this puzzle, just work backwards. If the lily pad completely covers the pond on day 60, then half the pond was covered on day 59, and one-quarter of the pond was covered on day 58.

Three Coin Flips

The following game has a $10 entry fee. You are to flip a fair coin three times. The first time it comes up heads you are paid $5. The second time it comes up heads you're paid an additional $7. The third time it comes up heads you're paid $9 more, for a possible maximum prize of $21. Would you pay the $10 entry fee to play?

If not, what would be a fair price for this game? Click below for the answer.

It's not a good idea to play this game at the offered entry fee. Here are the eight possible outcomes when flipping a coin three times, along with how much you would win after each flip.

When you subtract out the $10 entry fee, you only win "big" ($11) one out of eight times. Three times you win only $2, three times you lose $5, and one out of the eight times you lose your entire $10 entry fee. If you average these, you can expect to lose $1 every time you play. So, if you lower the entry fee to $9 this would be a fair game.

This problem appeared as an exercise in Introductory Graph Theory by Gary Chartrand.
See my Probability GitHub repository for a script that shows how to model this problem in Python.

One equals 0.999...

The following is a mathematical proof that 1 is equal to 0.999.... What's wrong with it? Click below for the answer.

$x = 0.999...$
$10x = 9.999...$
$10x = 9 + 0.999...$
$10x = 9 + x$
$9x = 9$
$x = 1$

There's nothing wrong with it. 1 really is equal to 0.999...

Two equals one?

The following is a mathematical proof that two equals one. What's wrong with it? Click below for the answer.

$a = b$
$aa = ab$
$aa - bb = ab - bb$
$(a + b)(a - b) = b(a - b)$
$a + b = b$
$a + a = a$
$2a = a$
$2 = 1$

The problem is in the fourth step, where both sides of the equation are divided by $(a - b)$. Since $a = b$ is given at the start, $a - b$ is 0, and you can't divide by 0.

State Names

There's only one letter in the English alphabet that is not used in the name of any of the 50 United States. Do you know which letter it is? Click below for the answer.

If you said 'J' or 'Z' you weren't far off. Each of those letters appear only once in the names of the 50 states (thanks to New Jersey and Arizona). The correct answer, though, is the letter Q, which does not appear in any state name.

To find the solution, I used a Python script to load a list of state names and count the occurrence of each letter of the alphabet. This method takes a lot less time than consulting a map.

Tic-Tac-Toe

In a standard game of Tic-Tac-Toe, players take turns placing X's and O's on a 3x3 grid until one player makes three-in-a-row in any direction (horizontally, vertically, or diagonally). Because of these rules, you can only place a maximum of five of either symbol on the board during a game, often ending in a draw.

Can you place six X's on a Tic-Tac-Toe board without making three-in-a-row in any direction? (Without placing any O's.) Click below for the solution.

I found the solution below with a little trial and error. The trick to this puzzle is that you cannot solve it with an X in the center position.

Draw Two

Two numbers are drawn at random from the integers 1 through 10. What is the expected value of their sum? Does it change if the second draw is done with or without replacement? Click below for the answers.

This puzzle is from Patrick Honner. It's easy to calculate the expected value with replacement. It's just two times the expected value of a random draw from 1...10, so 2 * 5.5, or 11. The interesting part is that when you draw two numbers without replacement the expected sum doesn't change. Why is that?

To find out, take a look at what happens to the expected value of the second draw for each value of the first draw. (Expected value is just the average of the remaining numbers.)

1st draw	E(2nd draw)
$1$	$6$
$2$	$5\frac{8}{9}$
$3$	$5\frac{7}{9}$
$4$	$5\frac{2}{3}$
$5$	$5\frac{5}{9}$
$6$	$5\frac{4}{9}$
$7$	$5\frac{1}{3}$
$8$	$5\frac{2}{9}$
$9$	$5\frac{1}{9}$
$10$	$5$

As the value of the first draw increases, the expected value of the second draw decreases. If you take the sum of each column you get 55. Divide by 10 to get the average and you get 5.5, so when you add them together you arrive back at the solution of 11.

See my Probability GitHub repository for a script that shows how to model this problem in Python.

Chicken McNuggets

You drove for hours last week to get your hands on McDonald's limited edition Szechuan sauce, and now you need some chicken nuggets for you and all of your friends. You can buy McNuggets in boxes of 6, 9, and 20. What is the largest whole number of nuggets that it is not possible to obtain by purchasing some combination of boxes of 6, 9, and 20? Click below for the answer.

There might be cleverer solutions to this problem, but we can do this fairly easily by listing combinations. Once we hit a streak of six numbers in a row that we can obtain, we know that the last number we couldn't obtain before the streak is the largest such number. Beyond that streak of six we can just add one or more boxes of 6 nuggets to one of those numbers to obtain any higher number. (There may be other combinations to obtain some of these numbers, but we only need one combination for each.)

Number	Boxes
1	Not Possible
2	Not Possible
3	Not Possible
4	Not Possible
5	Not Possible
6	6
7	Not Possible
8	Not Possible
9	9
10	Not Possible
11	Not Possible
12	6 + 6
13	Not Possible
14	Not Possible
15	6 + 9
16	Not Possible
17	Not Possible
18	9 + 9
19	Not Possible
20	20
21	6 + 6 + 9
22	Not Possible
23	Not Possible
24	6 + 9 + 9
25	Not Possible
26	20 + 6
27	9 + 9 + 9
28	Not Possible
29	20 + 9
30	6 + 6 + 9 + 9
31	Not Possible
32	6 + 6 + 20
33	6 + 9 + 9 + 9
34	Not Possible
35	6 + 9 + 20
36	9 + 9 + 9 + 9
37	Not Possible
38	9 + 9 + 20
39	6 + 6 + 9 + 9 + 9
40	20 + 20
41	6 + 6 + 9 + 20
42	6 + 9 + 9 + 9 + 9
43	Not Possible
44	6 + 9 + 9 + 20
45	9 + 9 + 9 + 9 + 9
46	6 + 20 + 20
47	9 + 9 + 9 + 20
48	6 + 6 + 9 + 9 + 9 + 9
49	9 + 20 + 20

That's six in a row, so we can get any higher number of nuggets just by adding boxes of 6 to those combinations. That means that 43 is the largest number of Chicken McNuggets that you cannot buy by combining boxes of 6, 9, and 20.

Pennies

Would you rather have a ton of pennies, four miles of pennies lined up end-to-end, or a stack of pennies half a mile tall? Click below for a hint, or for the answer.

One penny weighs 2.500 grams (according to the U.S. Mint).
There are about 28.35 grams in an ounce
There are 16 ounces in a pound.
There are 2,000 pounds in a (U.S.) ton.

One penny is 0.750 inches in diameter.
There are 12 inches in a foot.
There are 5,280 feet in a mile.

One penny is 1.52 millimeters thick.
There are 25.4 millimeters in an inch.

Four miles of pennies lined up end-to-end would be $3,379.20, while one ton is $3,628.80, so between the first two options you would be better off to take the ton. However, a stack of pennies half a mile tall would be $5,293.89, so the stack is by far the best option.

Western Leaders

Here's a freaky coincidence about World War II. If you add up the year of birth, age in 1944, year of taking power, and the number of years in office in 1944 for each of the five main leaders of the Western world during World War II, the sums are all the same.

	Churchill	Hitler	Mussolini	Roosevelt	Stalin
Year of birth	1874	1889	1883	1882	1878
Age in 1944	70	55	61	62	66
Took power	1940	1933	1922	1933	1922
Years in office	4	11	22	11	22
Sum	3,888	3,888	3,888	3,888	3,888

Can you explain this coincidence? Click below for the answer.

There's really no coincidence at all. If you take any person's year of birth and add their age in 1944, the sum will be... 1944. This also goes for the year a leader took office and the number of years they had held office in 1944, so the sum of all four values will always be 1944 + 1944 = 3888. You can make your own puzzle using any year as a reference point.

Concentric Shapes

See the image below of a square inscribed inside a circle inscribed inside a square. If the outer square has an area of 100 square inches, is there a quick way of figuring out the area of the inner square? Click below for the answer.

Spin the inner square around so the corners touch the top, bottom, and sides of the outer square.

Now imagine taking each corner of the outer square and folding them in so they touch in the center of the image. It's easy to see that the area outside the inner square will perfectly cover the area inside, so the inner square has exactly half the area of the outer square, or 50 square inches.

Digit Frequency

If you write down all the numbers from 1 to 1000 (inclusive) which digit occurs most frequently? Which digit appears least frequently in the same range? Click below for the answers.

You could write all the numbers down or write a program to count the digit frequencies, but this problem is much easier if you look for a pattern. The digits 0 through 9 all appear the same number of times in the ones place, but 1 through 9 appear a lot more often in the tens and hundreds place (because of numbers like 22, 222, etc., and the fact that we don't write leading 0s). This means that 0 is the least frequent digit. It only appears 192 times in the specified range. What about the most frequent? The digits 1 through 9 appear with exactly the same frequency in the range 1 to 999 (300 times each), so that extra occurrence (in the number 1000) makes 1 the most frequent digit from 1 to 1000.

Counting Chickens

If one-and-a-half chickens lay one-and-a-half eggs in one-and-a-half days, how many eggs does one chicken lay in one day? Click below for the answer.

For many people, the intuitive answer is one egg, but it pays double-check your math on this kind of problem. The daily rate of eggs per chicken per day is given by the formula

daily rate = eggs / (chickens x days)

Plugging in the numbers from the first part of the problem, we get

daily rate = 1.5 / (1.5 x 1.5)
daily rate = 1.5 / 2.25
daily rate = 2/3

So, one chicken lays two-thirds of an egg in one day.

Number Sense

How good is your "number sense"? How many of the following can you answer without using a calculator or looking up a conversion factor?

1. Are there more inches in a mile, or Sundays in 1000 years?
2. Are there more seconds in a week, or feet in 100 miles?
3. Are there more millimeters in a mile, or seconds in a month?
4. Which is larger, multiplying all the numbers from 1 to 10, or multiplying just the even numbers from 1 to 16?
5. Which is longer, 666 days or 95 weeks?
6. Which is longer, 666 inches or 55 feet?
7. Which is longer, 666 hours or 28 days?
8. Are there more ounces in a ton or inches in a kilometer?
9. Which is hotter, $0^{\circ}C$ or $0^{\circ}F$?
10. Which is larger, $e^\pi$ or $\pi^e$?

Click below for the answers.

1. Inches in a mile. (63,360. There can be up to 52,178 Sundays in 1000 years.)
2. Seconds in a week. (604,800, compared to 528,000 feet in 100 miles.)
3. Seconds in a month. (Even if the month only has 28 days, that's 2,419,200 seconds, compared to only 1,609,340 millimeters in a mile.)
4. Just the even numbers from 1 to 16. (Multiplying all the numbers from 1 to 10 gives you 3,628,800. Multiplying the even numbers from 1 to 16 give you 10,321,920.)
5. 666 days. (95 weeks is only 665 days.)
6. 666 inches. (55 feet is 660 inches.)
7. 28 days (which is 672 hours).
8. Inches in a kilometer. (39,370.1, compared to 35,840 ounces in a long ton, which is the heaviest ton.)
9. $0^{\circ}C$ is "hotter" since it is equal to $32^{\circ}F$
10. $e^\pi$ (23.14) is larger than $\pi^e$ (22.46).

Replacing Marbles

We place 15 black marbles and 15 white marbles in an urn. We have 30 additional black marbles in a bag. Then we follow these rules.

1. Remove two marbles from the urn.
2. If they are different colors, put the white marble back in the urn and the black marble in the bag.
3. If they are the same color, put both marbles in the bag, then put one black marble from the bag into the urn.

Continue following these rules until only one marble is left in the urn. What color is that marble? Click below for the answer.

When I first heard this puzzle, I immediately thought of writing a Python script, since that's my favorite method for dealing with problems in probability. This is a logic problem in disguise, though. I realized that as I tried to figure out the best way to set up the problem in code. If you pay close attention to the rules for adding and removing marbles from the urn, and the initial conditions, you'll notice a couple of things.

1. You start with an odd number of both black and white marbles in the urn.
2. The rules force you to always keep an odd number of white marbles in the urn (they can only be removed two at a time), but allow for both odd and even numbers of black marbles.

From those observations it's easy to see that when you get down to one marble, it must be a white marble.

Factor Sums

Not counting itself, the number 6 has the factors 1, 2, and 3, which add to 6. The number 28 has the same property (its factors are 1, 2, 4, 7, and 14). Can you come up with a three-digit number that has this property? What about a four-digit number? Click below for the answers.

If you knew that a number that is the sum of its own proper divisors is called a Perfect number, this puzzle was pretty easy. You could just search for that name and find the solutions are 496 and 8,128. Perfect numbers have been known at least as far back as Euclid (323–283 BCE), who included a formulation for then in his book of Elements.

The formulations states that $q(q + 1) / 2$ is a perfect number whenever $q$ is a prime of the form $2^p - 1$ for prime $p$ (now known as a Mersenne prime). So, if we know the first few Mersenne primes, we can calculate the first few perfect numbers.

$3(3 + 1) / 2 = 6$
$7(7 + 1) / 2 = 28$
$31(31 + 1) / 2 = 496$
$127(127 + 1) / 2 = 8,128$
$8,191(8,191 + 1) / 2 = 33,550,336$

The ancient Greek mathematicians would not have known that 8,191 was a prime, so Euclid would only have known the first four Perfect numbers. Now you can say you know something that Euclid didn't!

Minimum Percentage

75% of men from a certain group are tall, 75% have brown hair, and 75% have brown eyes. What is the minimum percentage that are tall, have brown hair, and have brown eyes? Click below to see the answer.

Instead of thinking in percentages to solve this problem, it's helpful to think back to the Pigeonhole Principle. Think of a group of 100 men, then 75 are tall, 75 have brown hair, and 75 have brown eyes. That's 225 individual attributes to assign to 100 men, so at least 25 of them (or 25%) must have each of the three attributes.

A Two-Digit Number

Find a two-digit number that's equal to two times the result of multiplying its digits. Click below to see the answer.

My first attempt at solving this puzzle was to set it up as an equation and try to solve it algebraically. Let's say the two digits are $x$ and $y$. Then the equation would be:

$10x + y = 2xy$

The left-hand side is the two-digit number ($x$ in the tens place, $y$ in the ones place) and the right-hand side is two times the result of multiplying its digits. If you try to isolate either $x$ or $y$, you'll see that it's not very easy to come up with a clean solution. That's because the equation above describes a hyperbola.

That's not exactly a dead end, but it isn't the kind of easy-to-understand (once you see it) solution I like in a logic puzzle. Luckily, there's an easier way. There aren't that many possibilities (we're only dealing with two digits), and we can eliminate a lot of them.

For example, we know that neither digit is 0. Also, we know that $2xy$ is an even number, so $y$ must be even (because the result of adding it to an even number is even). We also know that the product of the digits must be less than 50, otherwise $2xy$ would have three digits. That gets us down to only 32 possibilities to test.

Any other shortcuts that I can think of would only eliminate a few possibilities, but it's easy to just test the remaining ones (I went through them manually, but you could write a short script or use a spreadsheet), and find that the solution is

$36 = 2 * 3 * 6$

Identical Twins

Alice and Eve are identical twin sisters. One always lies and the other always tells the truth, but we don't know which is which. We ask one of them "Is Alice the one that always lies?" and she replies "Yes." Did we speak to Alice or Eve? Click below to see the answer.

We spoke to Eve. A person who always lies or always tells the truth cannot admit that they are a liar, so Alice could not have answered "Yes" to that question. (Note that we still don't know which sister is the liar and which is the truth teller.)

Counting Socks

All my socks are red except two. All my socks are white except two. All my socks are blue except two. How many socks do I have? Click below for the answer.

Oddly, I only have three socks. Don't let the fact that socks normally come in matching pairs distract you. No other number satisfies all three conditions above.

Circumnavigation

From 1519 until 1522, Ferdinand Magellan's Victoria was the first ship to successfully circumnavigate the globe. (Magellan himself did not survive the entire voyage.) Can you tell me which part of the ship traveled the greatest distance? Click below for the answer.

If you remembered the Rope Around the Earth puzzle I posted a few months ago, you probably got this one pretty quickly. Since the world is roughly spherical, the tip of the tallest mast of the ship would have traveled the greatest distance in sailing around the globe. Imagine if a boat sailed in a perfect circle around the equator. The part of the boat deepest under water (the keel) would create a smaller circle than the tip of the mast several feet above the water, so the tip of the mast travels the greatest distance during the voyage.

Replica of the Victoria, Photograph by Gnsin - Own work, CC BY-SA 3.0

50 factorial

50! = 30414093201713378043612608166064768844377641568960512071337804000

Without doing the full computation, can you tell whether the above statement is true or false? Click below for the answer.

You can probably guess that the statement is false, otherwise it wouldn't be much of a puzzle. The reasoning, though, is that the factorial for 50 must include the factors 10, 20, 30, 40, and 50, so it must end in at least five zeroes. The value above ends in only three zeroes, so it cannot be correct. (The correct value is 30414093201713378043612608166064768844377641568960512000000000000.)

The Missing Fish

Two fathers took their sons fishing. Each man and his son caught one fish, but when they all returned to camp they only had three fish. None of the fish were eaten, lost, or thrown back. How could this be? Click below to see the answer.

There were only three people on the fishing trip. One man was the father and grandfather of the other two.

Bags of Marbles

You have three identical bags, each containing two marbles. Bag A contains two white marbles, Bag B contains two black marbles, and Bag C contains one white and one black marble. You pick a bag at random and draw out one marble. If the marble is white, what is the probability that the other marble in the same bag is also white? Click below to see the answer.

Many people will instinctively answer 50%, or 1/2, since the marble has two possible colors, but the probability is actually 2/3 (66.67%). Why? If the first marble is white, then you know you didn't randomly select Bag B. That means that the first marble you selected has three (not two) possibilities:

1. The first marble in Bag A.
2. The second marble in Bag A.
3. The white marble in Bag C.

Only in the third case will the other marble be black, so there's a 2/3 probability that when the first marble is white, the second marble will also be white.

If you want to see how you would model this problem in Python, you can look at my solution on GitHub.

The Monk and the Mountain Path

One morning at precisely 9:00 AM a monk begins walking up a mountain path. He takes his time, stopping several times to rest along the way. He arrives at the temple at the mountain's summit at precisely 5:00 PM that evening. The next day, the monk leaves the temple at precisely 9:00 AM and makes his way back down the path. Again, he takes his time and rests at several points along the journey. He arrives back at his original starting point at precisely 5:00 PM that evening. Is there any time when the monk is in exactly the same spot on both days? Click below to see the answer.

Since the monk isn't travelling at a constant rate of speed on his two trips, it's tempting to say that there's not necessarily a time when the monk is in the same spot at the same time on both days. However, such a time and place must exist. To see why, take a look at the following plot of the two trips.

Imagine that you can grab the lines on the plot and bend them however you like, you just can't move the endpoints, and the lines must stay within the bounds of the two axes. No matter how you stretch and bend the lines, they must cross somewhere.

To think of it another way, imagine there were two monks, one at the base of the mountain and one at the temple, and they started their journeys on the same day. If they were to begin and end their trips at the same time, they would have to pass each other on the path at some point during the day.

The Pigeonhole Principle

The pigeonhole principle states that if a group of pigeons flies into a set of pigeonholes, and there are more pigeons than pigeonholes, then there must be at least one pigeonhole with two pigeons in it. More generally, if k + 1 or more objects are placed into k boxes, then there is at least one box containing two or more of the objects. Despite its seeming simplicity (perhaps obviousness), it can be used to solve a surprising range of problems in probability, number theory, and computer science, just to name a few. See if you can use it to solve the following three problems.

1. (Warm up) A drawer contains a dozen blue socks and a dozen black socks, all unmatched. If the room is dark, how many socks do you have to take out to be sure you have a matching pair?
2. Prove that there are at least two people in Tokyo with exactly the same number of hairs on their heads.
3. Prove that if five distinct integers are selected from the numbers 1 through 8, there must be at least one pair with a sum equal to 9.

Click below to see the answers.

1. (Warm up) If you've only heard one problem involving the pigeonhole principle, it was probably the classic sock drawer problem. You only need to pick three socks to make sure you have one matching pair. When you pick two socks, you might already have a matching pair, or you might have one of each color sock. Selecting one more sock ensures that you have at least two socks of one color or the other.
2. The Tokyo hairs problem sounds like something you might be asked as a "brain teaser" interview question. If you're stuck in an interview, then the first step is to show off your estimating skills. Since we're not in that situation, we can just use Google to find out that there are about 100,000 hairs on the average human head, and that Tokyo is home to about 13.6 million people. That's more than enough people for our proof. For the sake of simplicity, let's say that 200,000 is the maximum number of hairs a person can have on their head. Then, if you select 200,001 people who happen to each have a distinct number of hairs on their heads (zero is a valid number of hairs to have on your head), you only need one more to ensure that two people have the same number of hairs. (Note: This puzzle will work with any city larger than 200,001 residents.)
3. To see how the pigeonhole principle applies to this problem, you just need to group the numbers 1 through 8 in pairs that sum to 9. {1,8}, {2,7}, {3,6}, {4,5}. Now, if I select four distinct numbers from that range, I might select one number from each of the four pairs. If I select a fifth number, then I must complete one of the pairs that sums to 9.

Coffee with Cream

Suppose you have two cups in front of you, one with precisely 8 fluid ounces of coffee, and the other with precisely 8 fluid ounces of cream. You take precisely one teaspoon of the cream and add it to your coffee. You stir it in so that it's thoroughly mixed. Then you take precisely one teaspoon of that coffee/cream mixture and put it back into the cup of cream. Does the cup of coffee have more cream in it, or does the cup of cream contain more coffee? Click below for the answer.

This question is a bit tricky. It's tempting to think that the cup of coffee contains more cream, because the teaspoon of cream added to the coffee was 100% pure, while the teaspoon of coffee added to the cream was diluted. However, it's important to remember that the total volume of each vessel changed by one teaspoon after the first transfer of fluid. The coffee/cream mixture was greater by two teaspoons than the pure cream. Before I reveal the answer, let's re-frame the question in discrete units.

Suppose that instead of liquids, our two cups contained 20 black marbles and 20 white marbles. You take 5 white marbles and thoroughly mix then in with the black marbles. Then you randomly select 5 marbles from the black/white marble mixture and place them back in the cup of white marbles. Are there more white marbles in the black cup or more black marbles in the white cup?

If you're like me, you may be tempted to treat this as a probability problem, but it isn't one. When I think about randomly drawing marbles, I want to immediately start writing a quick simulation in Python, but as you'll see, that isn't necessary. We can easily enumerate all possible outcomes in this scenario to find the answer to the question. When we draw 5 marbles from the cup with a mixture of 20 black and 5 white marbles, then place them in the cup with the other 15 white marbles, there are only 6 possible outcomes:

black	white	black/white mix	white/black mix
5	0	15/5	15/5
4	1	16/4	16/4
3	2	17/3	17/3
2	3	18/2	18/2
1	4	19/1	19/1
0	5	20/0	20/0

So the black/white ratio of the 5 marbles in the second transfer doesn't really matter. The end result is that there are always the same number of white marbles in the black cup as there are black marbles in the white cup.

The same is true of the original coffee/cream problem. The ratio of the two liquids in the teaspoon that is transferred to the cup of cream is such that you will end up with precisely the same volume of coffee in your cream as there is cream in your coffee. So the answer to the trick question posed at the beginning is "neither, they are the same."

Letter Groupings

The letters of the (English) alphabet can be grouped into four distinct categories.

A M

B C D E K

F G J L

H I

Based on the categories established by the first 13 letters, can you place each of the remaining 13 letters in the correct group?

This question is tricky because it's not about the sounds the letters make, or the frequency of letters, but about the shapes of the (capital) letters.

The categories are:

A M T U V W Y (left-right mirror images)

B C D E K (top-bottom mirror images)

F G J L N P Q R S Z (no symmetry)

H I O X (symmetry about both axes)

Number Words

In the solution to A Unique Number, I asked a bonus question. "Can you think of a number whose letters when spelled out in English are all in alphabetical order?" Several people replied via Twitter with the correct answer of "forty." You may have found a shortcut to the solution if you noted that none of the single-digit numbers have their letters in alphabetical order, nor does the word "teen." This allows you to skip ahead to 20, 30, etc. Can you use a similar strategy to answer the following questions?

• What is the lowest number that requires the five vowels A, E, I, O, and U only once each in its spelling?
• What is the lowest number that requires the six letters A, E, I, O, U, and Y only once each in its spelling?

Click below to see the answers.

The lowest number that requires the five vowels A, E, I, O, and U once each in its spelling is 206 (two-hundred and six).

The lowest number that requires the six letters A, E, I, O, U, and Y once each in its spelling is 230 (two-hundred and thirty).

The strategy to quickly find these answers is to note which vowels are used in the base numbers, one, two, three, etc, then avoid combinations that include multiples of the same vowel. For example, you can skip past the 100s entirely, because "one-hundred" contains two of the letter "e".

The Nine Dot Puzzle

The following is a classic "thinking outside the box" puzzle. Can you connect all nine dots below by drawing exactly four straight lines, without lifting your pencil or tracing back over any line?

Give it a try before you click below for the answer.

If this puzzle looks familiar, it's because it dates back at least as far as Sam Loyd's 1914 Cyclopedia of Puzzles. When I said this was a classic "thinking outside the box" puzzle, that was a clue. You have to think outside the bounds of the box created by the nine dots to come up with a solution.

Apples and Oranges

You work in a factory boxing fruit. In front of you are three boxes labeled "apples," "oranges," and "apples & oranges." One box contains only apples, one contains only oranges, and one contains a mixture of both apples and oranges. Unfortunately, the label machine has gone haywire and has mislabeled all three boxes. Can you look at one piece of fruit from only one of the boxes and correctly label all three? Click below for the solution.

The key to this puzzle is that the type of fruit you pull from the box is not the only piece of information you have to work with. You also have the three labels that you know are incorrect. Pull a piece of fruit from the box labeled "apples & oranges." If it is an apple, then you know that this is the apples-only box. That means that the box (incorrectly) labeled "oranges" must be the box with both apples and oranges, and the box labeled "apples" must contain only oranges.

(It's interesting to note that if you pick from either the box labeled "apples" or the box labeled "oranges," you can't figure out the composition of the box. Only selecting from the box labeled "apples & oranges" leads to a solution.)

Common Thread

What do the following words have in common?

• dust
• seed
• left
• resign
• weather
• sanction

Click below to see the answer.

Each word has at least two meanings, and in each case one of those meanings is the opposite of the other.

• dust - as a verb can mean either to add or remove something.
• seed - also means either to add or remove something. If you seed the lawn you add seeds, but if you seed a tomato you remove them.
• left - can mean either remaining or departed.
• resign - can mean "to quit" but can also mean "to sign up again."
• weather - can mean "to withstand or make through" (weather the storm) or can mean "to be worn away."
• sanction - can mean 'give official permission or approval for (an action)' or conversely, 'impose a penalty on.'

For these and more, see the Mental Floss article 25 Words That Are Their Own Opposites.

Marking a Ruler

A 13-inch ruler only needs four markings on it so that it can be used to measure any whole number of inches from 1 to 13. At what positions should the four markings be? (Do not include the two ends, which are understood to be markings 0 and 13.) Click below to see the answer.

The markings should be at the 1, 2, 6, and 10-inch positions. Use the following markings to measure each whole-number length:

1 inch: 0 to 1
2 inches: 0 to 2
3 inches: 10 to 13
4 inches: 2 to 6
5 inches: 1 to 6
6 inches: 0 to 6
7 inches: 6 to 13
8 inches: 2 to 10
9 inches: 1 to 10
10 inches: 0 to 10
11 inches: 2 to 13
12 inches: 1 to 13
13 inches: 0 to 13

Move One Digit

The following equation is incorrect. Can you make the equation balanced by moving only a single digit?

101 - 102 = 1

Click below to see the answer.

The digit that needs to be moved is the 2. Just move it up into the exponent and the equation is correct.

101 - 10² = 1

What is the next number in the sequence?

Without Googling it, can you tell me the next number in the following sequence?

1
11
21
1211
111221
312211
13112221
1113213211

That should be enough to see the pattern, but this sequence goes on infinitely. Click below to see the answer.

This sequence is known as the "Look and Say" or "Say What You see" sequence. Each term is formed by describing the previous term. The first term is just the digit 1. To describe it you would say "one one," so the next term is 11. To describe that you'd say "two one," and so on. The next term after the ones shown is 31131211131221. Check the Online Encyclopedia of Integer Sequences (A005150) for more terms following that.

Beer Run

A man runs n laps around a circular track with a radius of t miles. He says he will drink s quarts of beer for every mile he runs. How many quarts will he drink? Click below for the answer.

He will only need one quart, no matter how far he runs. If the radius of the track is t miles, then the circumference is 2*pi*t miles. The man will run n laps, so the total distance is 2*pi*n*t miles. If he drinks s quarts per mile, then the total amount of beer is 2*pi*n*t*s, which equals one quart!

10-digit Number

Find a 10-digit number where the first digit is how many 0's there are in the number, the second digit is how many 1's in the number, the third digit is how many 2's, and so on, until the tenth digit which is how many 9's there are in the number.

Click below to see the answer.

As a programmer, I'm often tempted to try to use a brute force approach to find the answers to number puzzles. That often works, but when brute force involves looping through all 10-digit numbers, you should probably look for a more elegant approach.

Let's see if we can construct the solution using logic instead. We can't have 0 zeroes, because then we would have to put 0 in the zeroes digit, and it would immediately be wrong. I'll start with a 9 in the zeros digit and the rest zeros, then make corrections until we hit on a solution.

90000 00000

Now we have a 9, so there should also be a 1 in the 9 column.

90000 00001

But now there aren't 9 zeroes, there are only 8. There's also a 1, which means we have to change the first and second digits.

81000 00001

Wait, now there isn't a 9, so we have to move that last 1 over. There are also two 1's, so we have to change the second digit.

82000 00010

That's closer, but now there is a 2, so we have to record it in the twos column. There are also fewer 0's, so we have to change the first digit as well.

72100 00010

Still not quite right. There are now only six 0's, so we have to change the first digit again. There's also no longer an 8. We can make both of these changes at once, giving us a final answer of

62100 01000

The Extra Dollar

Here is an old math puzzle that you can find many versions of online.

Two friends have a meal at a restaurant, and the bill is $25. The friends pay $15 each, which the waiter gives to the cashier. The cashier gives back $5 to the waiter. The friends tell the waiter to keeps $3 as a tip, so he hands back $1 to each of the two diners.

So, the friends paid $14 each for the meal, for a total of $28. The waiter kept $3, and that makes $31. Where did the extra dollar come from? Give yourself a moment to think about it before clicking below for the solution.

$25 is sitting with the cashier, $2 is back with the diners, and $3 is with the waiter. That adds to the required $30, so there really is no extra dollar.

The mistake is expecting that what the diners paid and what the waiter kept to add up to what they initially gave. Adding $28 and $3 is just a bit of sleight-of-hand. It's the amount that the meal effectively cost them (including tip), plus the amount they received back, that should add to $30.

Arranging Eights

Can you arrange eight 8's so that when added they will equal 1000? Click below to see the answer.

It's certainly possible to try all 22 different ways to partition eight identical digits, but there is a shortcut.

All of the numbers that are created by arranging eight 8's will end in the digit 8, and the sum of the last digits of those numbers must be a multiple of 10 (because the target sum of 1000 ends in 0), so we know there must be exactly five groups of digits in the correct solution. That means we only have to check 3 different partitions of the eight digits.

8888 + 8 + 8 + 8 + 8
888 + 88 + 8 + 8 + 8
88 + 88 + 88 + 8 + 8

These are the only three ways to partition eight identical objects into five groups, and they are the only groupings whose sums end in the digit 0. You can check with quick mental arithmetic that the second grouping is the correct solution.

A Unique Number

What is unique about the number 8,549,176,320? Click below to see the answer (and a bonus question).

There's nothing numerically particularly unique or interesting about the number above. It is made up of all of the digits from 0 to 9, but a lot of numbers have that property. The unique thing about this number is that all of the digits from 0 to 9 are in alphabetical order when spelled out in English.

Bonus question: Can you think of a number whose letters when spelled out in English are all in alphabetical order? Example: The first three letters of the word "five" are in alphabetical order, but the "e" at the end spoils it.

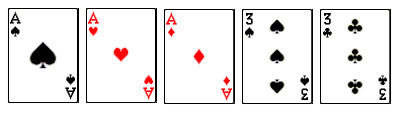
Best Poker Hand

Which of the following poker hands is the best? Assume one standard 52-card deck is used. The game is five-card draw, so there are no community cards, with no wild cards.

1. 
2. 
3. 
4. 
5. 

For reference, here are the rankings of poker hands.

• Royal flush - A, K, Q, J, 10, all the same suit.
• Straight flush - Five cards in a sequence, all the same suit.
• Four of a kind - Four cards all of the same rank.
• Full house - Three of a kind with a side pair.
• Flush - Any five cards, all the same suit
• Straight - Five cards in a sequence, any suits.
• Three of a kind - Three cards all of the same rank.
• Two pair - Two different pairs.
• One pair - Two cards of the same rank.
• High card - Highest card in your hand.

Click below to see the answer.

Hand #1 is the highest-ranking hand shown, but since all of these hands cannot occur on the same deal, it isn't the best hand to have in a real game.

To determine which hand is best, you have to look at how many other hands can beat each hand when dealt from the same deck. All of the hands above can be beaten by the same number of four-of-a-kinds, but by different numbers of straight flushes. Having two sixes as your side pair breaks up more of these possible straight flushes than having two kings, so hand #4 is actually the best hand to have. (There are 32 possible straight flushes that beat the kings hand, but only 24 that beat the sixes.)

The Collapsing Bridge

The bridge will collapse in 17 minutes! Four people need to cross the bridge before it collapses. It is a dark night and they have only one flashlight among them.

Only two people can cross at a time.

• Alice takes one minute to cross.
• Bob takes two minutes.
• Carol takes five minutes
• Dave takes 10 minutes to cross.

How can they all get across before the bridge collapses? Click below to see the answer.

The trick to this puzzle is to get the slowest members of the group to cross only once together, while the fastest members cross back and forth multiple times.

1. Alice and Bob cross first using up 2 minutes.
2. Alice comes back making it 3.
3. Carol and Dave cross together making it 13 minutes.
4. Then Bob crosses back, making it 15 minutes.
5. Finally, Alice and Bob cross together to make it a total of 17 minutes.

The Island of Knights and Knaves

Raymond Smullyan, one of the grand masters of logic puzzles, sadly passed away at the age of 97 earlier this week. In his honor, I present a classic puzzle adapted from his book What Is the Name of This Book?

There is a wide variety of puzzles about an island in which certain inhabitants called "knights" always tell the truth and others called "knaves" always lie. It is assumed that every inhabitant of the island is either a knight or a knave.

In this problem, there are only two people, A and B, each of whom is either a knight or a knave. A makes the following statement: "At least one of us is a knave." What are A and B?

Click below for the solution.

The solutions to these puzzles are often found by making one or more assumptions, then reasoning out whether or not it can be true. In this case, assume A is a knave. Then the statement "At least one of us is a knave" would be false, since knaves always lie. Hence, both A and B would be knights, which is impossible because we started with the assumption that A is a knave. Therefore, A must be a knight, and the statement "At least one of us is a knave" must be true, and B is a knave.

Raymond Smullyan presented a couple more of his puzzles in a 1982 interview on the Tonight Show with Johnny Carson. When you see the white hair and long beard, it seems like even 35 years ago that Smullyan was an old man, but the twinkle in his eye and the playfulness in his voice reveal that he was always a child at heart. Watch the full interview below.



If these puzzles seem too easy, they're just a small sample of Dr. Smullyan's brilliant work. If you really want a challenge, I encourage you to check out some of his books, or The Hardest Logic Puzzle Ever, also credited to Smullyan.

Finally, I leave you with a quote.

Why should I be worried about dying?
It's not going to happen in my lifetime!

-Raymond Smullyan (1919 - 2017)

Animal Kingdom

What do the following animals all have in common?

• firefly
• jackrabbit
• koala bear
• prairie dog
• silkworm
• guinea pig

Click below to see the answer.

All of the animals listed above are impostors.

• The firefly is not a fly. It is a beetle.
• The jackrabbit is not a rabbit. It is a hare.
• The koala is not a bear. It is a marsupial.
• The prairie dog is not a dog. It is a rodent.
• The silkworm is not a worm. It is a caterpillar.
• The guinea pig is not a pig. It is a rodent. (And it's not even from Guinea, a country on the west coast of Africa. Guinea pigs originated in the Andes mountains in South America.)

Name this Book

When this book first came out, it was only read by a handful of rather wealthy people. Now almost everyone has a copy, and many people read it regularly. You cannot buy it from a bookstore or borrow it from the library. Can you name this book? Click below for the answer.

It's a phone book.

This is a good example of an old riddle that has not aged well, so don't feel bad if you found it a bit tricky. Newer technology has rendered phone books practically useless, yet I still get one delivered to my house every year. In another generation or so, many people might not know what they were used for.

The Brodie Helmet

At the outbreak of World War I, none of the combatant nations provided steel helmets to their troops. Soldiers of most nations went into battle wearing cloth or leather hats that offered little protection from modern weapons. As a result, many soldiers suffered head injuries from exploding shrapnel.

In April of 1916, British soldiers began using a metal helmet in battle called the Brodie helmet, but authorities discovered that the proportion of head injuries then increased. Why should the incidence of head injuries increase when soldiers wore metal helmets rather than cloth caps? Click below to see the answer.

The number of recorded head injuries did increase after the introduction of the Brodie helmet, but the number of deaths decreased. Prior to the introduction of metal helmets, if a soldier were hit in the head with a piece of shrapnel, it would have likely killed him. This would have been recorded as a death, not a head injury. More head injuries were recorded after the helmets were introduced due to the simple fact that more soldiers were surviving them.

Panama Canal

A ship sailed through the Panama Canal going from west to east. When it exited the canal, it entered the Pacific Ocean. (The ship did not double back.) How can this be so? Click below to see the answer.

Normally when we think about the American continents, we think of the Pacific Ocean being to the west and the Atlantic Ocean to the east, but that isn't strictly the case. Panama is an isthmus that curves, and the Panama Canal was constructed so that it runs from the Caribbean Sea on the northwest end to the Pacific Ocean on the southeast. In the age of instant access to world maps, this "puzzle" is probably a lot easier to verify now than when the canal was originally built.

Rope Around the Earth

Suppose you tie a rope tightly around the Earth at the equator. (Assume the Earth is perfectly spherical, and that the surface is smooth so that the rope lies tight against the surface at all points.) Now suppose that you add an additional 6 feet to the length of the rope. How high off the surface would the rope lie? You could look up the Earth's circumference and do the math to come up with an exact answer, but can you quickly come up with an intuitive guess? (High enough to slide a piece of paper under? To wave your hand under? To walk under?) Click below to see a hint or the answer.

Hint: If I reversed the parameters and told you that I increased the length enough to raise the rope 6 feet from the surface in all directions, could you tell me how much was added to the length of the rope? (Given the formula for the circumference of a circle, C = 2πr, but not knowing the circumference of the Earth, can you come up with a guess?) Reversing that, can you come up with the answer to the original problem?

Answer: The first time they hear this puzzle, many people will try to do the math starting with the circumference of the Earth. That doesn't matter though. It's a property of any circle that if you increase the circumference by a fixed amount, the radius will change by that amount divided by 2π (because r = C/2π). The rope could be tied around a beach ball or a tennis ball and the answer would not change. So the exact answer to the problem is 0.95493 feet, but if you said "about 1 foot" you were right.

Voyageurs

I've been reading The Revenant by Michael Punke and came across the following few passages. The main character, Hugh Glass, is embarking on a canoe trip up the Missouri River with a group of French Canadian fur traders known as voyageurs.

...For the rest of their voyage, Glass manned not a paddle but an enormous sponge, constantly bailing water as it pooled on the bottom of the canoe.

It was a full-time job, since the bâtard leaked steadily. The canoe reminded Glass of a floating quilt. Its patchwork skin of birch bark was sewn together with wattope, the fine root of a pine tree. The seams were sealed with pine tar, reapplied constantly as leaks appeared. As birch had become more difficult to find, the voyageurs were forced to use other materials in their patching and plugging. Rawhide had been employed in several spots, stitched on and then slathered in gum. Glass was amazed at the fragility of the craft. A stiff kick would easily puncture the skin, and one of La Vierge's main tasks as steersman was the avoidance of lethal, floating debris. At least they benefited from the relatively docile flow of the fall season. The spring floods could send entire trees crashing downstream.

If you've ever maintained a large code base, you probably already see where I'm going with this. The constant patching and plugging of leaks, the fragility of the craft, one man constantly bailing out water while several others row the boat guided by a steersman. These elements all remind me of several large software projects I've been on.  The passage continues.

There was an upside to the bâtard's shortcomings. If the vessel was frail, it was also light, an important consideration as they labored against the current. Glass came quickly to understand the odd affection of voyageurs for their craft. It was a marriage of sorts, a partnership between the men who propelled the boat and the boat that propelled the men. Each relied upon the other. The voyageurs spent half their time complaining bitterly about the manifold ails of the craft, and half their time nursing them tenderly.

This reminds me not only of the relationship programmers have with our code, but also of the relationship we have with our tools. How much time do we spend complaining about an IDE or a framework? How much time configuring them? But after we've gotten comfortable using them, most of us will strongly resist switching to a new one. Finally...

They took great pride in the appearance of the bâtard, dressing it in jaunty plumes and bright paint. On the high prow they had painted a stag's head, its antlers tilted challengingly toward the flowing water. (On the stern, La Vierge had painted the animal's ass.)

This final bit surprises me the most, but in a way I suppose it shouldn't. I don't know much about boating, but I do know that you should fix the leaks in your boat before you bother to decorate it. But that isn't how we always approach software development, is it? I've seen people spend plenty of time refactoring and cleaning code that didn't really need to change, or adding test cases just to get a higher percentage in test coverage. At times I've been guilty of this myself. I guess it's worth it to ask yourself, before you make a change to your code, am I fixing a leak, or am I just painting a stag's ass on this canoe?